

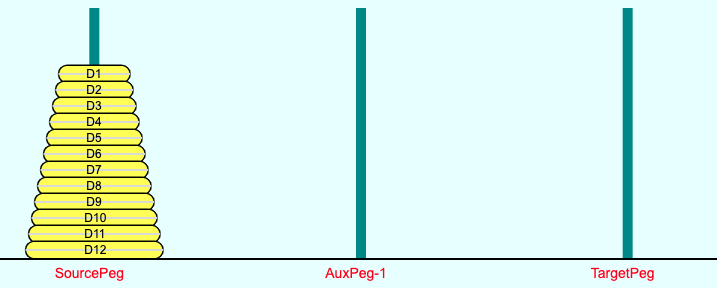
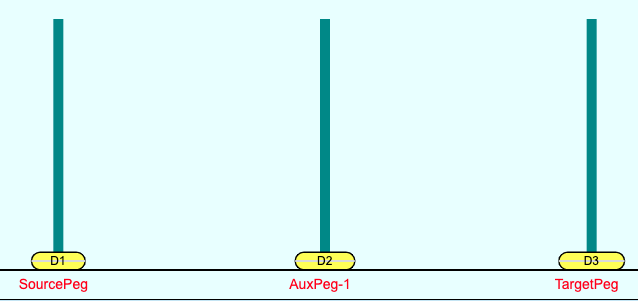
The “Tower of Hanoi” is a well-known puzzle. It contains 3 Pegs - A Source-Peg, an Auxiliary-Peg, and a Target-Peg. A peg is just a vertical cylindrical rod. All 3 Pegs have the same diameter. A disk is flat and cylindrical in cross section and has a hole in the center, with a hole diameter matching the diameter of the pegs. Any number of these disks are stacked on the Source-Peg. The disks are stacked in the order of decreasing disk diameter, so that the bottom-most disk in the stack has the largest diameter and the top-most disk has the smallest diameter. The initial state of the Tower Of Hanoi puzzle with 3 Pegs is as shown in Figure 1 below.
The goal of the puzzle is to move the entire stack of disks from the Source-Peg to the Target-Peg. In the end state all disks should be on the Target-Peg in the same order as they are on the Source-Peg. The Auxiliary-Peg is used as a working Peg to hold the disks as you work your way from the initial state to the end state. This goal - going from initial state to end state - must be achieved with the minimum number of moves, while adhering to the following two rules.
The simplest case of this puzzle has only 1 disk on the Source-Peg. The solution is of-course trivial - just 1 move - move the single disk from the Source-Peg to the Target-Peg - see Figures 2 and 3 below. Since there is only 1 disk, the two rules mentioned above are trivially satisfied, and the number of moves cannot possibly be less than 1.
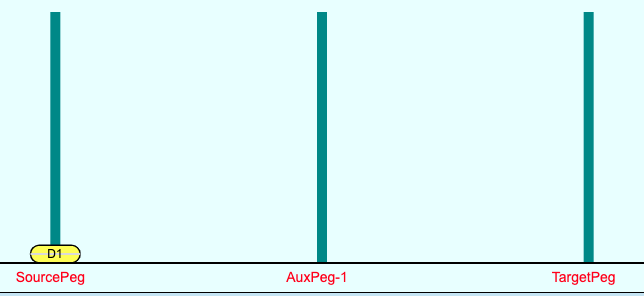
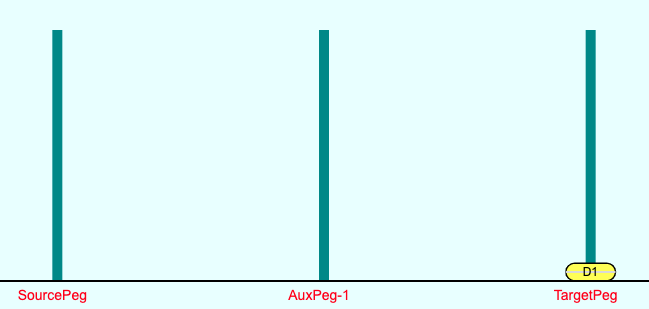
Despite being trivial, this solution forms the basis of the solutions for all cases with higher number of disks, because of a principle known as “Recursion”.
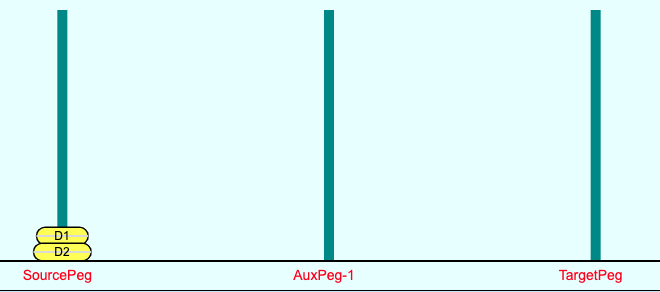
Consider the case of 2 disks. We can simplify the two disk case as follows. The disk D1 - resting on top of the larger diameter disk D2 - must be moved first. However, we cannot move D1 directly to the Target-Peg, because if we do that, then the larger diameter disk D2 cannot be placed on top of D1 on the Target-Peg. In the end state, the disk D2 must be at the bottom of the stack on the Target-Peg. Therefore, the first step must be to move the disk D1 from Source-Peg to Auxiliary-Peg. In effect the original Auxiliary-Peg is temporarily playing the role of Target-Peg, and the Original Target-Peg is temporarily playing role of Auxiliary-Peg - see Figures 4 and 5 below.
With disk D1 out of the way, the Source-Peg now contains just the larger disk D2, and the end state demands that D2 be at the bottom of the stack of the Target-Peg, which is currently empty. So again step 2 is nothing but the trivial solution to 1 disk puzzle, with no change in the roles of the pegs - see Figures 5 and 6 below. The presence of the disk D1 in the Auxiliary peg does not make any difference to the step 2.

Now in step 3, all we need to do is move disk D1 from the Auxiliary-Peg to the Target-Peg to reach the final state of the 2 disk Tower of Hanoi. Since disk D1 is smaller than disk D2, step 2 automatically obeys Rule 2 above. Again, please observe that step 3 is nothing but the trivial solution to 1 disk puzzle, with the Original Auxiliary-Peg temporarily acting as the Source-Peg and the Original Source-Peg temporarily acting as the Auxiliary-Peg - see Figures 6 and 7 above.
Please note that the entire solution to the 2 disk case of Tower of Hanoi is made up of three steps, each of which is the trivial solution of the 1 disk Tower of Hanoi as listed below. In the following discussion, we will use the term “top section of the Source-Peg stack” to represent the top disk D1 in the Source-Peg in the initial state.
Solution to Tower of Hanoi with 2 disks:
Step 1: Solve 1 Disk Tower of Hanoi (trivial solution) with the “top section of the Source-Peg stack” (top section = 1 disk) and the Peg roles: Original Source-Peg = Source-Peg, Original Auxiliary-Peg = Temporary Target-Peg, and Original Target-Peg = Temporary Auxiliary-Peg.
Step 2: Solve 1 Disk (trivial solution) with the “bottom-most disk in Source-Peg stack” (D2), no change in Peg roles.
Step 3: Solve 1 Disk Tower of Hanoi (trivial solution) with the “top section of the Source-Peg stack” (top section = 1 disk) and the Peg roles: Original Auxiliary-Peg = Temporary Source-Peg, Original Source-Peg = Temporary Auxiliary-Peg, and Original Target-Peg = Target-Peg.
Let us next consider the case of 3 disks. We can solve the 3 disk Tower of Hanoi in terms of the solution to the “2 disk Tower of Hanoi” and the trivial solution of the “1 disk Tower of Hanoi” in similar 3 steps as shown below.
Solution to Tower of Hanoi with 3 disks:
Step 1: Solve 2 Disk Tower of Hanoi (see above) with the “top section of the Source-Peg stack” (top section = 2 disks D1, D2) and the Peg roles: Original Source-Peg = Source-Peg, Original Auxiliary-Peg = Temporary Target-Peg, and Original Target-Peg = Temporary Auxiliary-Peg.
Step 2: Solve 1 Disk (trivial solution) with the “bottom-most disk in Source-Peg stack” (D3), no change in Peg roles.
Step 3: Solve 2 Disk Tower of Hanoi (see above) with the “top section of the Source-Peg stack” (top section = 2 disks D1, D2) and the Peg roles: Original Auxiliary-Peg = Temporary Source-Peg, Original Source-Peg = Temporary Auxiliary-Peg, and Original Target-Peg = Target-Peg.
Now, when you consider that step 1 of the 3 disk Tower of Hanoi solution, please realize that step 1 itself is made up of the 3 steps of the 2 disk Tower of Hanoi solution above. The switched Roles of the Auxiliary-Peg and Target-Peg in step 1 of the 3 disk Tower of Hanoi solution, are the input "Peg Roles" to the 2 disk Tower of Hanoi solution. And the 2 disk Tower of Hanoi, in turn switches the roles of the pegs again (relative to the input "Peg Roles"). Please convince yourself using the 4 Figures - 8, 9, 10, and 11 below, that the step 1 of the 3 disk Tower of Hanoi solution is indeed just the 2 disk Tower of Hanoi solution with the input "Peg Roles" of: Original Source-Peg = Source-Peg, Original Auxiliary-Peg = Temporary Target-Peg, and Original Target-Peg = Temporary Auxiliary-Peg.All "Peg role switches" must be relative to the input Peg Roles.
So in the Step 1 of the 3-Disk case, the Peg Roles are broken down into 3 sub-steps of the 2-Disk case as follows:
3-Disk-Step-1a: Original Source-Peg = Source-Peg, Original Auxiliary-Peg = Auxiliary-Peg, Original Target-Peg = Target-Peg.
3-Disk-Step-1b: Original Source-Peg = Source-Peg, Original Auxiliary-Peg = Temporary Target-Peg, Original Target-Peg = Temporary Auxiliary-Peg.
3-Disk-Step-1c: Original Source-Peg = Temporary Auxiliary-Peg, Original Auxiliary-Peg = Temporary Target-Peg,
Original Target-Peg = Temporary Source-Peg.
So, at the end of the 3-Disk-step 1, the two disk “top section of the Source-Peg stack” (disks D1 and D2)
ends up in the Auxiliary-Peg - which was acting as the Temporary Target-Peg in the 3-Disk-Step 1.

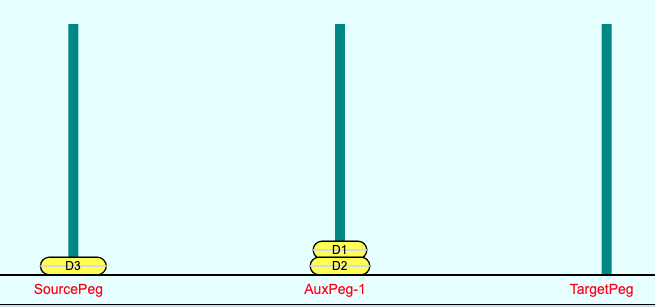
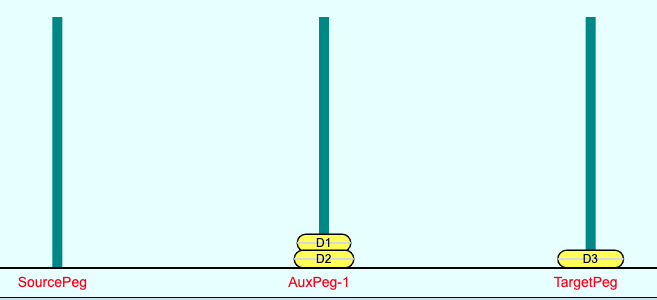
The Figure 12 and 13 below show the step 2 (trivial solution) of the 3 disk Tower of Hanoi with the bottom-most disk D3 being moved from Source-Peg to Target-Peg. Here the input "Peg Roles" to the same as the Original "Peg Roles" of the 3 Disk case.

In the step 3 of the 3 disk Tower of Hanoi solution again we have the same situation as step 1. The switched Roles of the Auxiliary-Peg and Source-Peg in step 3 of the 3 disk Tower of Hanoi solution, are the input "Peg Roles" to the 2 disk case, which in turn switches the roles of the pegs again (relative to the input roles).
Figures 14, 15, 16, and 17, below show the step 3 of the 3 disk Tower of Hanoi solution. Please walk through them to convince yourself that it is indeed just the 2 disk Tower of Hanoi solution with the input "Peg Roles" of: Original Source-Peg = Temporary Auxiliary-Peg, Original Auxiliary-Peg = Temporary Source-Peg, and Original Target-Peg = Target-Peg. So, at the end of step 3, the two disk “top section of the Source-Peg stack” (disks D1 and D2) get moved from the Original Auxiliary-Peg - which was acting as the temporary Source-Peg in step 3, to the Original Target-Peg, on top of the disk D3 that was moved to the Target-Peg in step 2.


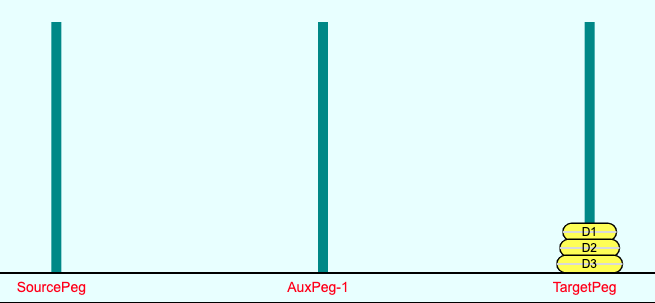
So, now we have a basis for the solution to the Tower of Hanoi with any number (n) of disks. The solution can be represented by the following 3 steps.
Solution to Tower of Hanoi with “n” number of disks:
Step 1: Solve (n-1) Disk Tower of Hanoi with the “top section of the Source-Peg stack”
(top section = (n - 1) disks D1, D2,…. D(n-1) ) and the Peg Roles:
Original Source-Peg = Source-Peg,
Orignal Auxiliary-Peg = Temporary Target-Peg, and Original Target-Peg = Temporary Auxiliary-Peg.
Step 2: Solve 1 Disk (trivial solution) with the “bottom-most disk in Source-Peg stack” (Dn), no change in Peg Roles.
Step 3: Solve (n-1) Disk Tower of Hanoi with the “top section of the Source-Peg stack”
(top section = (n - 1) disks D1, D2,…. D(n-1) ) and the Peg roles:
Original Auxiliary-Peg = Temporary Source-Peg,
Original Source-Peg = Temporary Auxiliary-Peg, and Original Target-Peg = Target-Peg.
In programming, this is called the principle of recursion. Here the solution for a case with parameter of positive integer n is expressed in terms of the solution to the case with parameter (n-1), and solution for the parameter (n-1) is expressed in terms of the solution to the case with parameter (n-2)… . and so on, until you reach the lowest parameter value - most often n = 1. The solution for the case of the lowest parameter value is often trivial. So, in a recursive solution, the program needs to implement only the code for the trivial solution of the lowest parameter value. For any case of higher parameter value n, the program (i.e., the function) simply re-executes itself with parameter value of (n - 1). This creates a stack of suspended function calls until the parameter value reaches n = 1. At that point the program executes the trivial solution and returns to the top suspended call in the stack of recursive calls. The stack of calls then unwinds and produces the solution to the case of parameter value n.
In the case of the recursive solution to Tower of Hanoi with n disks, it is important to realize that there is not just 1 stack of recursive calls, but a hierarchcy of multiple stacks at each level. This is so, because given the current recursion with the parameter parameter value of n, each recursive call with parameter value of (n - 1), spawns two stacks of recursive calls at the (n - 1) level: One stack for the Step 1 of the (n - 1) case and a separate stack of recursive calls for the Step 3 of the (n - 1) case. Again each of these two recursive calls spawns two more stacks of recursive calls at the (n - 2) level, and .... so on. At the base of each stack, the trivial solution gets executed, and the entire solution is made up of them.
The special feature of the recursive solution to the Tower of Hanoi is the requirement of switching Peg roles for each successive recursive call. In effect the “Peg Roles” are also a parameter of the function , and the value of this “Peg Roles” parameter changes in a predictable pattern (i.e., it is programmable) as we go from the n level to the (n - 1) level. Each successive recursive calls receives as input the number of disks i.e., (n - 1) and the “Peg Roles” parameter which can be computed from the "Peg Roles" of the current recursion at the n level.
How Many Total Moves for a Case with n Disks?
The number of moves needed for Tower of Hanoi with 1 disk (n = 1) is 1 move = 21 - 1 (see Figures 2 and 3).
The number of moves needed for Tower of Hanoi with 2 disks (n = 2) is 3 moves = 22 - 1 = 3 (see Figures 4, 5, 6, 7).
Consider the postulate: The number of moves needed for Tower of Hanoi with n disks is (2n) - 1.
The number of moves needed for Tower of Hanoi with (n + 1) disks can be formulated as:
Total Number of Moves needed for Tower of Hanoi with (n + 1) disks
= Number of moves needed in Step 1 of the Tower of Hanoi with n disks
+ Number of moves needed in Step 2 of the Tower of Hanoi with n disks
+ Number of moves needed in Step 3 of the Tower of Hanoi with n disks
But the number of moves for Step 1 and Step 3 will always be equal for any value of n because physically they are identical -
just moving n disks from one peg to another.
Also, since step 2 is always the trivial step of moving the bottom-most disk rom the Source-Peg to the Target-Peg, the
moves needed in Step 2 of the Tower of Hanoi with n disks is always 1 move.
Total Number of Moves needed for Tower of Hanoi with (n + 1) disks
= 2 * Number of moves needed in Step 1 of the Tower of Hanoi with n disks
+ 1 move for Step 2
= 2 * (2n - 1) + 1
= 2(n + 1) - 2 + 1
= 2(n + 1) - 1
So, the above postulate is verified for n = 1, and n = 2, and if we assume it to be correct for
n, then we proved it is correct for (n + 1).
This proves the above postulate. You need 2n - 1
moves for the solution to the Tower of Hanoi with n disks.